Did you ever wonder why Kdenlive’s smooth interpolation mode may overshoot between keyframes? And how to tell Kdenlive to avoid such situations?
I did wonder, and so I was starting to look behind the scenes and were introduced to the strange world of smoothness. Don’t worry, there won’t be any mathematics for you to learn and understand. Just watch the figures. 🙂 We’ll also show you how to avoid such overshots in those situations you don’t want it. And for the really curious what the mathematics behind “smooth” interpolation are: just see the end of this toolbox post.
The Fade-In Ramp
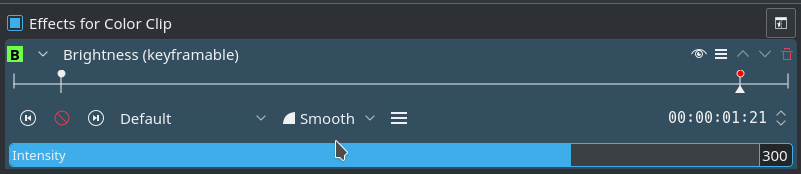
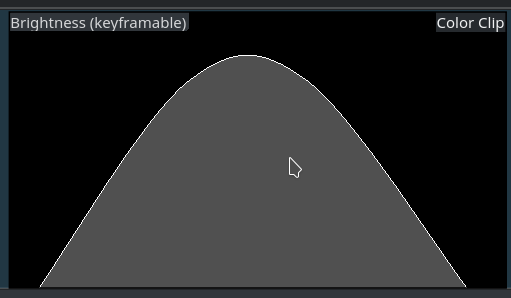
Let’s start with a simple ramp, as shown here. We use two keyframes, one with a low value setting, and the other with a high value setting. The particular values don’t matter. We set both keyframe to the interpolation mode smooth.
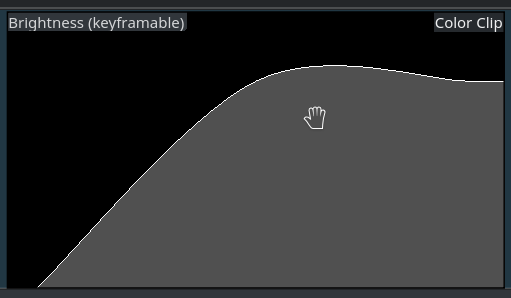
The effect display inside the timeline clip looks like a straight ramp. But if you watch the interpolated values closely while scrubbing the timeline, you should notice that the slope of the ram varies. At the end and beginning the slope is smaller than in the middle, where it is higher.
But what exactly is going on here?
So I discovered this sweet tool GeoGebra (Open Source) for trying out the Mathematics inside Kdenlive’s MLT engine.
Eh, no panic!
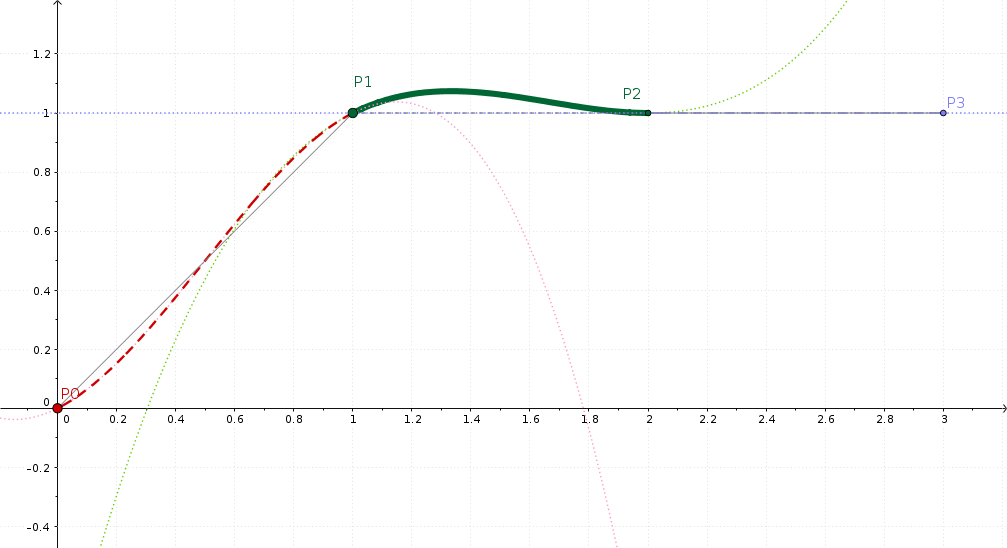
This figure shows two keyframes P1=0 and P2=1, which is a fairly typical ramp up setting. In case you already wonder: it doesn’t matter at which exact frames the individual keyframes are. If that sounds odd, it probably is. But this is how the underlying math works (you know: see the end for details).
The smooth interpolation that MLT will calculate is drawn as a thick green line. It’s bend a little bit like the capital letter S, but then, not really too much.
And if you look closely, then beginning and ending slope of the green line aren’t horizontal ‒ at least what I expected at first.
You may wonder what the two other keyframes P0 and P3 are good for? Well, the math underneath always require four keyframes in order to interpolate segment-wise between any two adjacent keyframes. And if there is no preceeding (P0) or trailing (P1) keyframe, then we’ll simple repeat the left (P1) or right (P2) keyframe.
Ramp-Up, and … Overshoot
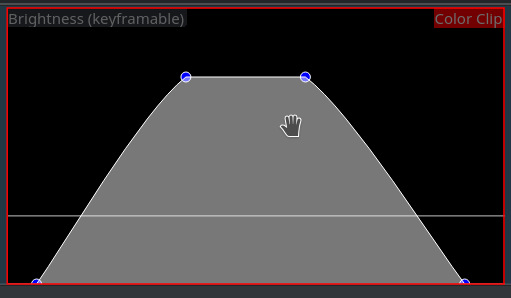
Now let’s add a third keyframe, so this looks like a ramp with a plateau. This is shown in the screen shots.
And now, the ramp gets a clearly visible bump instead of a sharp bend. Well, this looks smooth, but not exactly what we may have intended? So why is this the way it is?
This is now our ramp with a plateau: P0=0, P1=1, P2=2. Don’t worry about the keyframe numbering, though.
Did you expect the plateau to be, well a straight plateau? Me too. But you may have already notice that Kdenlive doesn’t exactly behave like this. Instead, the interpolation math causes the interpolated values to overshoot, as you can easily see in the figure.
What the underlying math does is this: the interpolation is smooth, so that the slope to the left of P1 is the same as to the right of P1. Yeah, that’s a slightly different “smooth” from what you might have been expecting.
If you want the plateau to be straight instead, then you must set the interpolation mode of the keyframe P1 to linear instead. By the way, tThis doesn’t change the previous smooth segment in any way. And this results in a “rough bent” at P1, but luckily you probably won’t notice in most situations.
Ramp Up-Flat-Down
Let’s add another, fourth keyframe, so we have: ramp-up first, then flat, then ramp-down. A fairly typical fade-in and fade-out keyframe template.
And look, what’s happening: we’ve good a hunch-back, but not a nice and flat middle section. Gosh!
This time, we look at the middle section P1-P2. To the left, we see the up ramp, to the right, the down ramp.
Again, smooth now means that there is no sharp bend in the segments. Instead, the left+right slopes are continuous at P1 and P2; that is, in the middle section. And this causes our interpolated value to overshoot. So awful. So sad. Shhh.
Make Flat Great Again
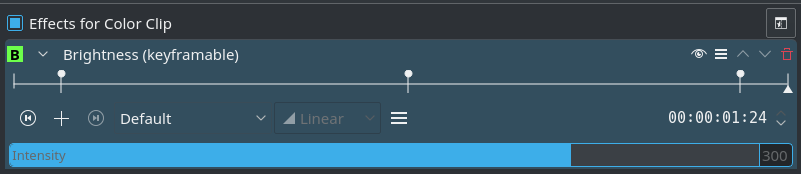
Now, how do we get a flat top? Fortunately, that’s easy to achieve, as you can see from the screenshots.
- first keyframe: smooth,
- second keyframe: interpolated(!),
- third keyframe: smooth,
- forth keyframe: interpolated (albeit that does not really matter if there are no further keyframes).
So great!
For the Curious (Furious?)
As you may (or rather may not) remember, Kdenlive’s rendering engine is the MLT Multimedia Framework. While MLT has smooth interpolation since around mid-2013, Kdenlive only later caught up and now supports all three interpolation modes linear, discrete, and finally smooth. As can be seen from the MLT source code, smooth interpolation is done using a Catmull-Rome spline. In particular, MLT uses the so-called “uniform” variant, because it is so simple. The downside is that this smoothing sometimes has the unwanted property of overshooting, especially when you least expect it.